Solving resistor networks
This application describes how to write a uLisp program to calculate the resistance of a resistor network such as:
11th February 2023: Updated with clearer instructions of how to install and run the program.
Running the program
To run the resistor network program you need a ARM, ESP, or RISC-V board running the appropriate 32-bit version of uLisp, with floating-point support.
- Download the appropriate version of uLisp from Download uLisp.
- Use the Arduino IDE to upload it to the board; see Download uLisp - Installing uLisp.
- Open the Serial Monitor in the Arduino IDE to display the uLisp prompt.
- Display the source of the resistor network program here: Resistor network program
- Select the text of the program, copy it, paste it into the Arduino IDE Serial Monitor input field, and press Return.
Defining the network
Describe the network you want to solve as a list specifying the resistance, in ohms, between each pair of nodes. Label each node with a letter, such as a, b, c, etc.
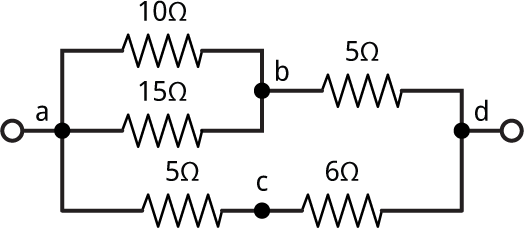
For example, the circuit shown above would be described as:
(defvar *circuit* '((a d ?) (a b 10) (b a 15) (b d 5) (a c 5) (c d 6)))
For example, (a b 10) specifies that a resistor of 10Ω is connected between nodes a and b. The order of the nodes isn't important.
The list (a d ?) represents the resistance we want to calculate.
- Type this definition into the Arduino IDE Serial Monitor input field, followed by Return.
Solving the network
- Run the program by typing the following command into the Arduino IDE Serial Monitor input field, followed by Return:
(solve *circuit*)
The solution will be printed as a list:
((d a 5.5) (a d ?))
So the network reduces to a single resistor between d and a of 5.5Ω.
How it works
Series and parallel
One way to calculate series and parallel resistors is to define Lisp functions:
(defun series (x y) (+ x y)) (defun parallel (x y) (/ (+ (/ x) (/ y))))
Note that in Lisp (/ x) is a shorter way of writing (/ 1 x).
Now we can use these functions to express the complete circuit:
> (parallel (series 5 6) (series (parallel 10 15) 5)) 5.5
and the answer is 5.5 Ω.
A more general way of representing a network
Using the serial and parallel functions requires the user to do most of the work. A more intuitive and general way to represent a resistor network would be to label each of the nodes a, b, c, etc and then represent it as a list of the resistances between each pair of nodes. Using this approach the above network becomes:
(defvar *circuit* '((a d ?) (a b 10) (b a 15) (b d 5) (a c 5) (c d 6)))
The list (a d ?) represents the resistance we want to calculate.
We can then write a program to progressively search for series or parallel configurations, and combine them.
All possible divisions of a set into two subsets
It will be useful to have a function split-set, that takes a list and an index i, and returns the ith division of the set into two subsets.
(defun split-set (lis i)
(let (in out (ll (reverse lis)))
(dotimes (j (length lis))
(if (oddp i) (push (nth j ll) in) (push (nth j ll) out))
(setq i (ash i -1)))
(list in out)))
For a list of length n the total possible number of subsets is 2n. The function split-set works by expressing the index i as a binary number, and it then puts each element into one of the two sets according to whether the bit corresponding to that element is a 0 or a 1. So, for example, 13 in binary is 1101 so the 13th split of the list of four elements (a b c d) is:
> (split-set '(a b c d) 13) ((a b d) (c))
Combining parallel and series resistors
To simplify the network we successively combine pairs of resistors according to the rules of parallel and series resistors. To do this we look at every possible pair of resistors and see if they can be combined into a single resistor. For example, the two parallel resistors between a and b could be merged into a single resistor.
Here's the routine series-parallel to combine two resistors x and y. It also takes the entire circuit as a parameter so we can check for other connections between the same nodes:
(defun series-parallel (l x y)
(cond
((or (eq (caddr x) '?) (eq (caddr y) '?))
nil)
;; Check four possible labellings
(t (let (result)
(dolist (x (list x (list (second x) (first x) (third x))))
(dolist (y (list y (list (second y) (first y) (third y))))
;; Resistors in parallel
(when (and (eq (first x) (first y))
(eq (second x) (second y)))
(setq result
(list
(list
(first x) (second x) (/ (+ (/ (third x)) (/ (third y))))))))
;; Resistors in series
(when (and (eq (first x) (first y))
(= (countlinks l (first x)) 2)
(not (eq (second x) (second y))))
(setq result
(list (list (second x) (second y) (+ (third x) (third y))))))))
result))))
For two resistors in parallel we simply need to check that their start and end nodes are the same. For example, here it combines the resistors between a and b:
> (series-parallel *circuit* '(a b 10) '(b a 15)) ((b a 6.0))
For two resistors in series we also need to check that no other resistor is connected to the node between the two resistors; this is what countlinks does:
(defun countlinks (l x)
(let ((n 0))
(mapc (lambda (i) (when (or (eq x (first i)) (eq x (second i))) (incf n))) l)
n))
For example, here we combine the two resistors between a, c, and d:
> (series-parallel *circuit* '(a c 5) '(c d 6)) ((a d 11))
If it's not possible to combine the resistors series-parallel returns nil:
> (series-parallel *circuit* '(a b 10) '(b d 5)) nil
Simplifying a circuit
To simplify a circuit we use split-set to check every possible pair of resistors to see if they can be combined by series-parallel:
(defun simplify (lis function n)
(let* ((l (length lis))
(k (expt 2 l)))
(dotimes (i k lis)
(let* ((s (split-set lis i))
(in (first s))
(out (second s)))
(when (= (length in) n)
(let ((c (apply function lis in)))
(when c (return (append c out)))))))))
This function simplify takes a list representing the network, a function for combining resistors, and a number of resistors to combine, and returns the simplified network.
Finally to solve the network we call simplify repeatedly until there's no more work to do:
(defun solve (circuit)
(let (len)
(loop
(setq len (length circuit))
(setq circuit (simplify circuit #'series-parallel 2))
(when (= (length circuit) len) (return)))
circuit))
Here it is working on the above network:
> (solve *circuit*) ((d a 5.5) (a d ?))
So the network reduces to a single resistor of 5.5Ω.
Networks containing triangles
Unfortunately there are some networks that this approach can't solve. For example:
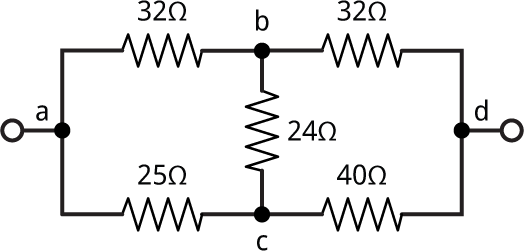
This can be represented as the list:
(defvar *c2* '((a d ?) (a b 32) (b c 24) (a c 25) (b d 32) (c d 40)))
Trying to solve it gives:
> (solve *c2*) ((a d ?) (a b 32) (b c 24) (a c 25) (b d 32) (c d 40))
It has failed to simplify it at all because the circuit doesn't contain any series or parallel configurations.
Delta-Wye transformations
The solution is to do what's called a Delta-Wye transformation, which converts a triangle configuration, or delta, into a Y or wye configuration by adding an extra node [1]:
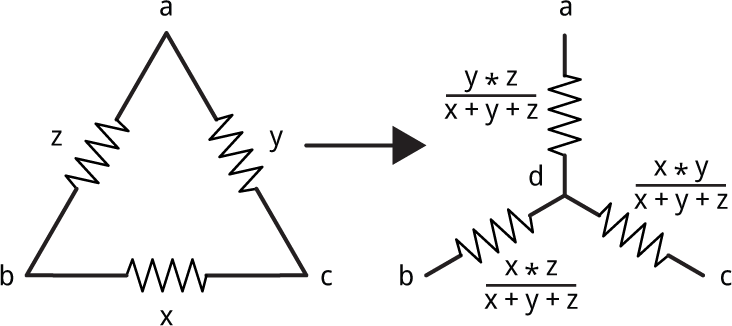
To solve these configurations the function delta-wye checks three links, and if they qualify as a delta network, they are transformed into a wye:
(defun delta-wye (l x y z)
(cond
((or (eq (caddr x) '?) (eq (caddr y) '?) (eq (caddr z) '?))
nil)
;; Check eight possible labellings
(t (let (result)
(dolist (x (list x (list (second x) (first x) (third x))))
(dolist (y (list y (list (second y) (first y) (third y))))
(dolist (z (list z (list (second z) (first z) (third z))))
(when (and (eq (first x) (second z))
(eq (first y) (second x))
(eq (first z) (second y)))
(let ((sum (+ (third x) (third y) (third z)))
(newsymbol (incf *newnode*)))
(setq result
(list
(list
(first x) newsymbol (/ (* (third x) (third z)) sum))
(list
(first y) newsymbol (/ (* (third x) (third y)) sum))
(list
(first z) newsymbol (/ (* (third y) (third z)) sum)))))))))
result))))
The function delta-wye labels the new node it creates with a unique integer, to distinguish it from the nodes in the original network:
(defvar *newnode* 0)
Testing it with x=1, y=2, and z=3 gives:
> (delta-wye nil '(a b 3) '(b c 1) '(c a 2)) ((a 1 1) (b 1 0.5) (c 1 0.333333))
where '1' is the new node it has created.
The solve function can be updated to incorporate delta-wye as follows:
(defun solve (circuit)
(let (len)
(loop
(setq len (length circuit))
(setq circuit (simplify circuit #'delta-wye 3))
(setq circuit (simplify circuit #'series-parallel 2))
(setq circuit (floating circuit))
(when (= (length circuit) len) (return)))
circuit))
I've also added a function floating to remove resistors with only one end connected to the network, which can arise from delta-wye transformations:
(defun floating (l)
(let (result)
(dolist (x l result)
(unless
(or
(= (countlinks l (first x)) 1)
(= (countlinks l (second x)) 1))
(push x result)))))
Testing the new version of solve on the network *c2*:
> (solve *c2*) ((a d 32.0) (a d ?))
and the resistance between a and d is 32Ω.
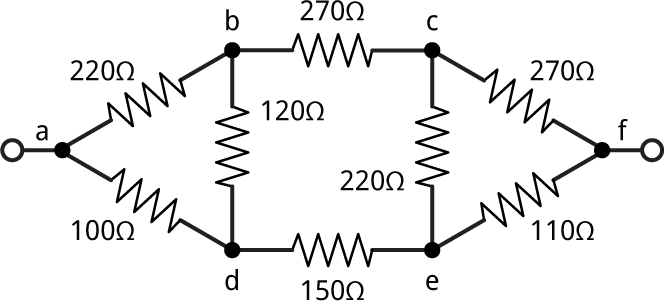
Another example
Finally, find the resistance between a and f in this network containing two deltas:
- ^ Delta-Wye resistor networks on Khan Academy.
