Plotting the Hofstadter Q sequence
The Hofstadter Q sequence is one of several recursive sequences described in Douglas Hofstadter's book "Gödel, Escher, Bach: an Eternal Golden Braid", and it's one of the functions in Benchmarks. It is defined as follows:
(defun q (n)
(if (<= n 2) 1
(+
(q (- n (q (- n 1))))
(q (- n (q (- n 2)))))))
It is related to the Fibonacci sequence, except that in this case the two preceding terms specify how far to go back in the sequence to find the two terms to be summed. If you print the first 16 terms, for n=1 to n=16 at first it looks like a slow version of the Fibonacci sequence:
> (dotimes (x 16) (format t "~a " (q (1+ x)))) 1 1 2 3 3 4 5 5 6 6 6 8 8 8 10 9
However (q 16) reveals a surprise; it's not monotonically increasing. A graph of the function reveals more of its erratic behaviour.
The graph
The following graph shows the behaviour of the first 240 elements of the Q sequence on a 240x135 colour TFT display:
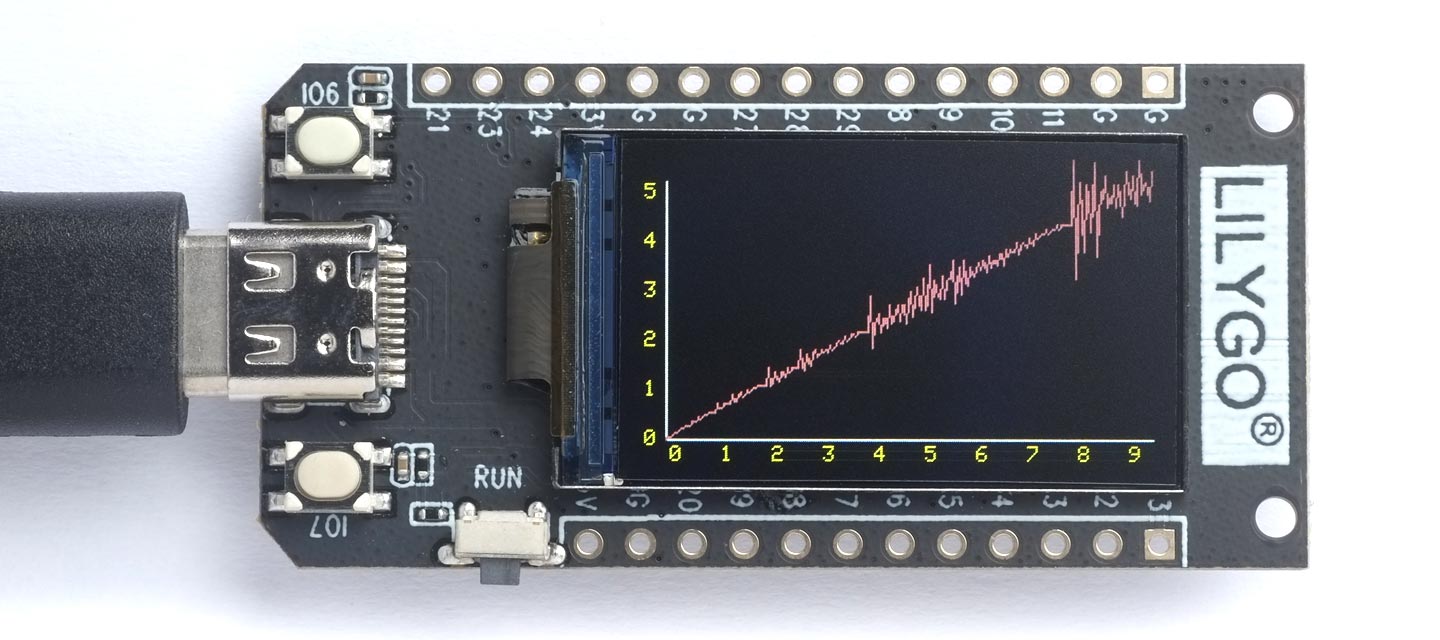
This is running on the LILYGO T-Display RP2040.
The program
Here's the program:
(defun q (n)
(if (<= n 2) 1
(+
(q (- n (q (- n 1))))
(q (- n (q (- n 2)))))))
(defun speedup (fn)
(let ((c nil))
(lambda (x)
(or (cdr (assoc x c))
(let ((r (funcall fn x)))
(setq c (cons (cons x r) c))
r)))))
(setq q (speedup q))
(defun qplot (width height)
(fill-screen)
(let ((x0 0) (y0 0) x1 y1
(yellow #b1111111111100000)
(salmon #b1111110000010000))
(draw-line 10 (- height 10) (1- width) (- height 10))
(draw-line 10 (- height 10) 10 10)
(dotimes (n 6)
(draw-char 0 (- height (* n (truncate height 6)) 14) (code-char (+ n 48)) yellow))
(dotimes (n 10)
(draw-char (+ (* n (truncate width 10)) 12) (- height 7) (code-char (+ n 48)) yellow))
(dotimes (n width)
(setq x1 n y1 (q n))
(draw-line (+ x0 10) (- height y0 10) (+ x1 10) (- height y1 10) salmon)
(setq x0 x1 y0 y1))))
The function q is highly recursive, so successive terms take longer and longer to calculate. The solution is to use the function speedup, which memoises q to create a version that only calculates each new term once. The function is memoised by evaluating:
(setq q (speedup q))
The function qplot plots the graph, with arbitrarily labelled axes. To plot the above graph call:
(qplot 240 135)
